Introduction
Optimization algorithms have emerged as powerful tools capable of finding the best possible solutions to complex problems. With their applications spanning across engineering, economics, computer science, and various other fields, these algorithms play a pivotal role in maximizing efficiency, minimizing costs, and achieving optimal outcomes. In this comprehensive article, we will delve into the different types of optimization algorithms, their strengths, and how they can be applied to solve real-world challenges.
Gradient-Based Methods: Navigating the Landscape of Optimization
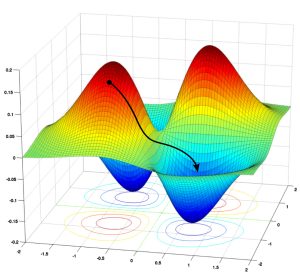
Gradient-based methods are among the most widely used optimization algorithms. These methods utilize derivatives to navigate the solution space and find the local optimal solution. By calculating the gradient of the objective function, these algorithms iteratively update the solution in the direction of steepest descent. With their efficiency and effectiveness, gradient-based methods have found extensive applications in machine learning, data analysis, and numerical optimization. However, it is important to note that they are limited to finding local optima and may struggle with non-smooth or discontinuous functions.
Metaheuristic Algorithms: Exploring the Search Space
In contrast to gradient-based methods, metaheuristic algorithms draw inspiration from natural phenomena and aim to explore a large solution space to find optimal solutions. These algorithms offer the advantage of being able to escape local optima and discover global optimal solutions. By intelligently exploring and exploiting the solution space, metaheuristic algorithms exhibit robustness and flexibility in tackling complex problems. One popular metaheuristic algorithm is Particle Swarm Optimization (PSO), which simulates the collective movement of particles to search for the best solution. Genetic Algorithm (GA) is another widely used metaheuristic algorithm that mimics the principles of genetics and evolution to iteratively improve the solution. Furthermore, Ant Colony Optimization (ACO) models the foraging behavior of ants to solve optimization problems, demonstrating the power of nature-inspired algorithms in optimization.
Evolutionary Algorithms: Mimicking Nature’s Selection Process
Evolutionary algorithms, a subset of metaheuristic algorithms, simulate the process of natural selection to search for optimal solutions. Inspired by Darwinian evolution, these algorithms evolve a population of potential solutions through generations, applying genetic operators such as mutation and crossover to explore and exploit the solution space. Genetic Programming (GP), Evolutionary Strategies (ES), and Differential Evolution (DE) are examples of evolutionary algorithms that have proven effective in solving complex optimization problems. By combining the principles of selection, reproduction, and variation, evolutionary algorithms provide a powerful framework for finding optimal solutions in diverse domains.
Hybrid and Ensemble Approaches: Combining Strengths for Enhanced Performance
In pursuit of even better optimization performance, researchers and practitioners often employ hybrid and ensemble approaches that combine multiple algorithms. These approaches leverage the strengths of different optimization techniques to overcome their individual limitations. For example, a hybrid approach may integrate a gradient-based method with a metaheuristic algorithm, allowing for efficient local exploration and global search capabilities. Ensemble approaches, on the other hand, involve running multiple optimization algorithms in parallel and combining their results to achieve improved solutions. By harnessing the complementary strengths of various algorithms, hybrid and ensemble approaches provide enhanced problem-solving capabilities.
Choosing the Right Algorithm for the Task
Selecting the most appropriate optimization algorithm depends on the characteristics of the problem at hand. Gradient-based methods excel in problems with smooth and continuous solutions, providing efficient convergence to local optima. Metaheuristic algorithms and evolutionary algorithms are better suited for problems with non-smooth, discontinuous, or combinatorial solution spaces. These algorithms have the ability to explore a wide range of possibilities and discover global optima. The choice of algorithm also depends on considerations such as computational resources, problem constraints, and time constraints. Researchers and practitioners must carefully evaluate the problem requirements to determine the most suitable optimization approach.
The Power of Optimization Algorithms
The benefits of optimization algorithms extend far beyond finding optimal solutions. These algorithms empower decision-makers to make informed choices, allocate resources effectively, optimize processes, and minimize costs. By leveraging the strengths of different algorithms, researchers and practitioners can tackle complex problems with confidence and achieve their objectives more efficiently. Moreover, the study and development of optimization algorithms have profound theoretical implications. These algorithms provide insights into the fundamental principles of mathematics, computer science, and nature-inspired processes. By exploring the behavior and performance of optimization algorithms, researchers continually advance our understanding of complex systems and problem-solving methodologies.
Conclusion
Optimization algorithms have emerged as invaluable tools that empower us to solve complex problems, optimize processes, and achieve optimal outcomes in various domains. With a wide range of algorithms at our disposal, from gradient-based methods to metaheuristic and evolutionary algorithms, researchers and practitioners can choose the most suitable approach for the specific characteristics of the problem. By harnessing the power of optimization algorithms, we can push the boundaries of what is possible, drive innovation, and overcome challenges in the pursuit of excellence. The continuous advancement and application of optimization algorithms promise a future where complex problems can be solved with unprecedented efficiency and effectiveness, revolutionizing industries and propelling us towards new frontiers of discovery.